总览
| 函数声明 | 函数功能 |
|---|---|
double cabs (double complex z); |
计算复数 z 的绝对值(double) |
float cabsf (float complex z); |
计算复数 z 的绝对值(float) |
long double cabsl (long double complex z); |
计算复数 z 的绝对值(long double) |
double creal (double complex z); |
计算复数z的实部(double) |
float crealf (float complex z); |
计算复数z的实部(float) |
long double creall (long double complex z); |
计算复数z的实部(long double) |
double cimag (double complex z); |
计算复数z的虚部(double) |
float cimagf (float complex z); |
计算复数z的虚部(float) |
long double cimagl (long double complex z); |
计算复数z的虚部(long double) |
double carg (double complex z); |
计算复数z的相位角 (double) |
float cargf (float complex z); |
计算复数z的相位角(float) |
long double cargl (long double complex z); |
计算复数z的相位角(long double) |
double complex cacos (double complex z); |
计算复数z的反余弦 (double complex) |
float complex cacosf (float complex z); |
计算复数z的反余弦(float complex) |
long double complex cacosl (long double complex z); |
计算复数z的反余弦(long double complex) |
double complex cacosh (double complex z); |
计算复数z的反双曲余弦(double complex) |
float complex cacoshf (float complex z); |
计算复数z的反双曲余弦(float complex) |
long double complex cacoshl (long double complex z); |
计算复数z的反双曲余弦(long double complex) |
double complex casin (double complex z); |
计算复数z的反正弦(double complex) |
float complex casinf (float complex z); |
计算复数z的反正弦(float complex) |
long double complex casinl (long double complex z); |
计算复数z的反正弦(long double complex) |
double complex casinh (double complex z); |
计算复数z的反双曲正弦(double complex) |
float complex casinhf (float complex z); |
计算复数z的反双曲正弦(float complex) |
long double complex casinhl (long double complex z); |
计算复数z的反双曲正弦(long double complex) |
double complex catan (double complex z); |
计算复数z的反正切(double complex) |
float complex catanf (float complex z); |
计算复数z的反正切(float complex) |
long double complex catanl (long double complex z); |
计算复数z的反正切(long double complex) |
double complex catanh (double complex z); |
计算复数z的反双曲正切(double complex) |
float complex catanhf (float complex z); |
计算复数z的反双曲正切(float complex) |
long double complex catanhl (long double complex z); |
计算复数z的反双曲正切(long double complex) |
double complex ccos (double complex z); |
计算复数z的余弦(double complex) |
float complex ccosf (float complex z); |
计算复数z的余弦(float complex) |
long double complex ccosl (long double complex z); |
计算复数z的余弦(long double complex) |
double complex ccosh (double complex z); |
计算复数z的双曲余弦(double complex) |
float complex ccoshf (float complex z); |
计算复数z的双曲余弦(float complex) |
long double complex ccoshl (long double complex z); |
计算复数z的双曲余弦(long double complex) |
double complex csin (double complex z); |
计算复数z的正弦(double complex) |
float complex csinf (float complex z); |
计算复数z的正弦(float complex) |
long double complex csinl (long double complex z); |
计算复数z的正弦(long double complex) |
double complex csinh (double complex z); |
计算复数z的双曲正弦(double complex) |
float complex csinhf (float complex z); |
计算复数z的双曲正弦(float complex) |
long double complex csinhl (long double complex z); |
计算复数z的双曲正弦(long double complex) |
double complex ctan (double complex z); |
计算复数z的正切(double complex) |
float complex ctanf (float complex z); |
计算复数z的正切(float complex) |
long double complex ctanl (long double complex z); |
计算复数z的正切(long double complex) |
double complex ctanh (double complex z); |
计算复数z的双曲正切(double complex) |
float complex ctanhf (float complex z); |
计算复数z的双曲正切(float complex) |
long double complex ctanhl (long double complex z); |
计算复数z的双曲正切(long double complex) |
double complex cexp (double complex z); |
计算复数z的指数基数e(double complex) |
float complex cexpf (float complex z); |
计算复数z的指数基数e(float complex) |
long double complex cexpl (long double complex z); |
计算复数z的指数基数e(long double complex) |
double complex clog (double complex z); |
计算复数z的自然对数(以e为底)(double complex) |
float complex clogf (float complex z); |
计算复数z的自然对数(以e为底)(float complex) |
long double complex clogl (long double complex z); |
计算复数z的自然对数(以e为底)(long double complex) |
double complex conj (double complex z); |
计算复数z的共轭(double complex) |
float complex conjf (float complex z); |
计算复数z的共轭(float complex) |
long double complex conjl (long double complex z); |
计算复数z的共轭(long double complex) |
double complex cpow (double complex x, double complex y); |
计算x的y次方值 (double complex) |
float complex cpowf (float complex x, float complex y); |
计算x的y次方值 (float complex) |
long double complex cpowl (long double complex x, long double complex y); |
计算x的y次方值 (double complex) |
double complex cproj (double complex z); |
计算复数z在黎曼球面上的投影(double complex) |
float complex cprojf (float complex z); |
计算复数z在黎曼球面上的投影(float complex) |
long double complex cprojl (long double complex z); |
计算复数z在黎曼球面上的投影(long double complex) |
double complex csqrt (double complex z); |
计算复数z的平方根(double complex) |
float complex csqrtf (float complex z); |
计算复数z的平方根(float complex) |
long double complex csqrtl (long double complex z); |
计算复数z的平方根(long double complex) |
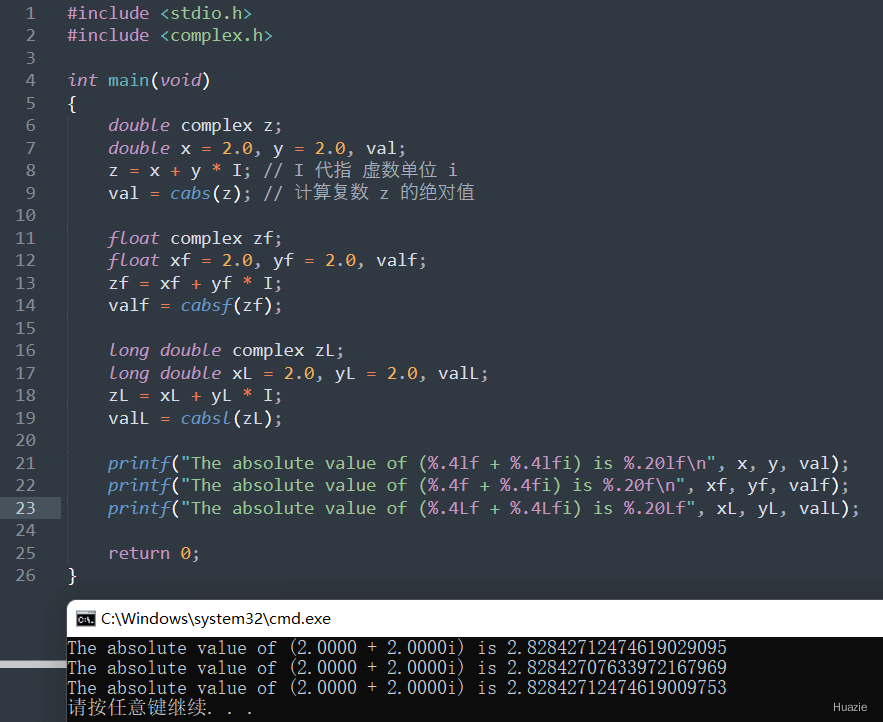
1. cabs,cabsf,cabsl
1.1 函数说明
| 函数声明 | 函数功能 |
|---|---|
double cabs (double complex z); |
计算复数 z 的绝对值(double) |
float cabsf (float complex z); |
计算复数 z 的绝对值(float) |
long double cabsl (long double complex z); |
计算复数 z 的绝对值(long double) |
1.2 演示示例
1 | // Huazie |
1.3 运行结果
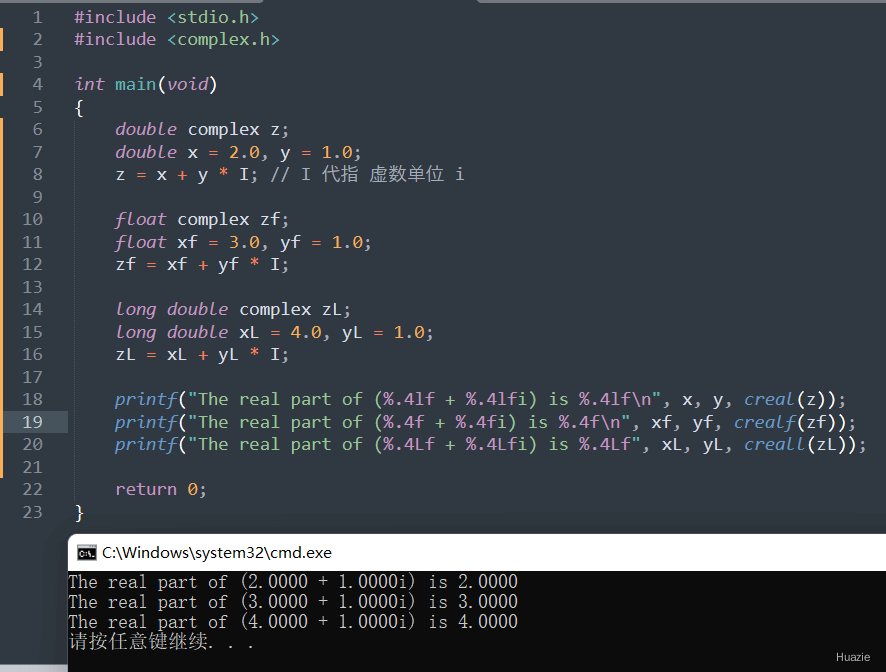
2. creal,crealf,creall
2.1 函数说明
| 函数声明 | 函数功能 |
|---|---|
double creal (double complex z); |
计算复数z的实部(double) |
float crealf (float complex z); |
计算复数z的实部(float) |
long double creall (long double complex z); |
计算复数z的实部(long double) |
2.2 演示示例
1 | // Huazie |
2.3 运行结果
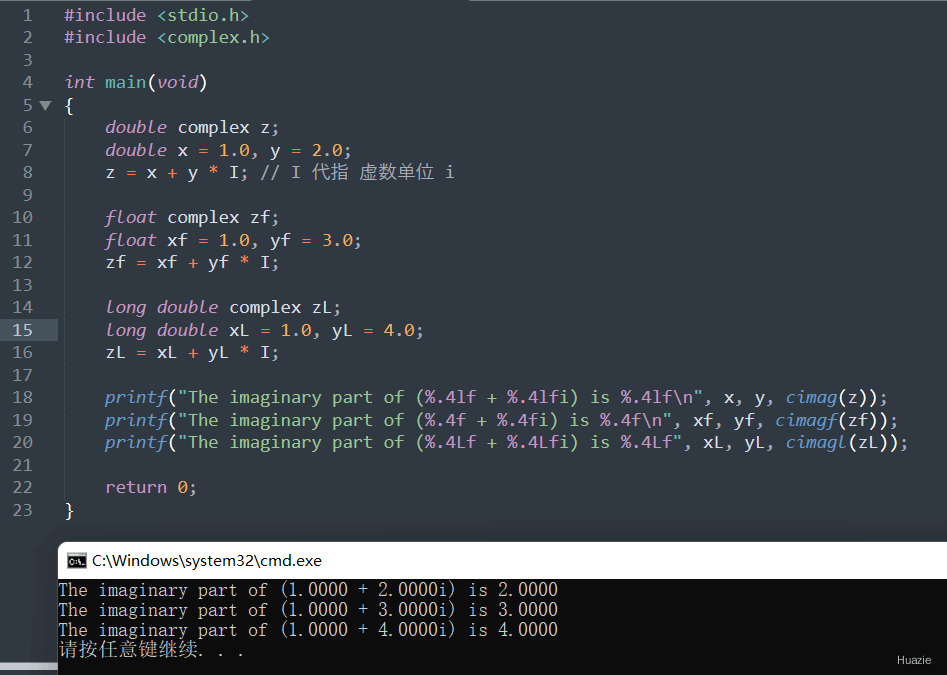
3. cimag,cimagf,cimagl
3.1 函数说明
| 函数声明 | 函数功能 |
|---|---|
double cimag (double complex z); |
计算复数z的虚部(double) |
float cimagf (float complex z); |
计算复数z的虚部(float) |
long double cimagl (long double complex z); |
计算复数z的虚部(long double) |
3.2 演示示例
1 | // Huazie |
3.3 运行结果
4. carg,cargf,cargl
4.1 函数说明
| 函数声明 | 函数功能 |
|---|---|
double carg (double complex z); |
计算复数z的相位角 (double) |
float cargf (float complex z); |
计算复数z的相位角(float) |
long double cargl (long double complex z); |
计算复数z的相位角(long double) |
相位角是描述波形在时间轴上的位置的一个重要参数,它决定了波形的起始位置和变化状态。在实际应用中,相位角的测量和控制对于电路设计和信号处理至关重要。通过对相位角的理解和应用,可以更好地分析和控制波动现象,从而实现对电力系统和通信系统的优化。
4.2 演示示例
1 |
|
4.3 运行结果
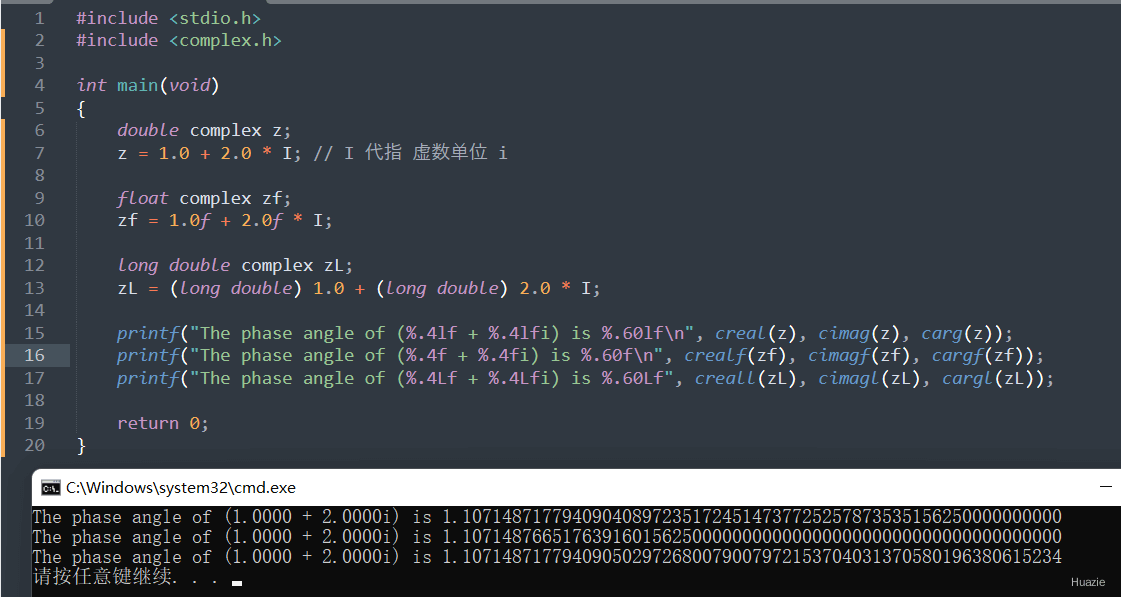
5. cacos,cacosf,cacosl
5.1 函数说明
| 函数声明 | 函数功能 |
|---|---|
double complex cacos (double complex z); |
计算复数z的反余弦 (double complex) |
float complex cacosf (float complex z); |
计算复数z的反余弦(float complex) |
long double complex cacosl (long double complex z); |
计算复数z的反余弦(long double complex) |
反余弦函数是三角函数中余弦函数的逆函数,其主要作用是在已知余弦函数值的情况下,求解对应的角度值。反余弦函数的定义域为[-1, 1],值域为[0, π]。
反余弦函数的图像是一个在[0, π]区间内单调递减的曲线。
- 当
x=1时,arccos(1)=0,表示余弦值为1的角度是0度; - 当
x=-1时,arccos(-1)=π,表示余弦值为-1的角度是180度。 - 随着x值从1减小到-1,
arccos(x)的值从0增加到π。
5.2 演示示例
1 |
|
5.3 运行结果
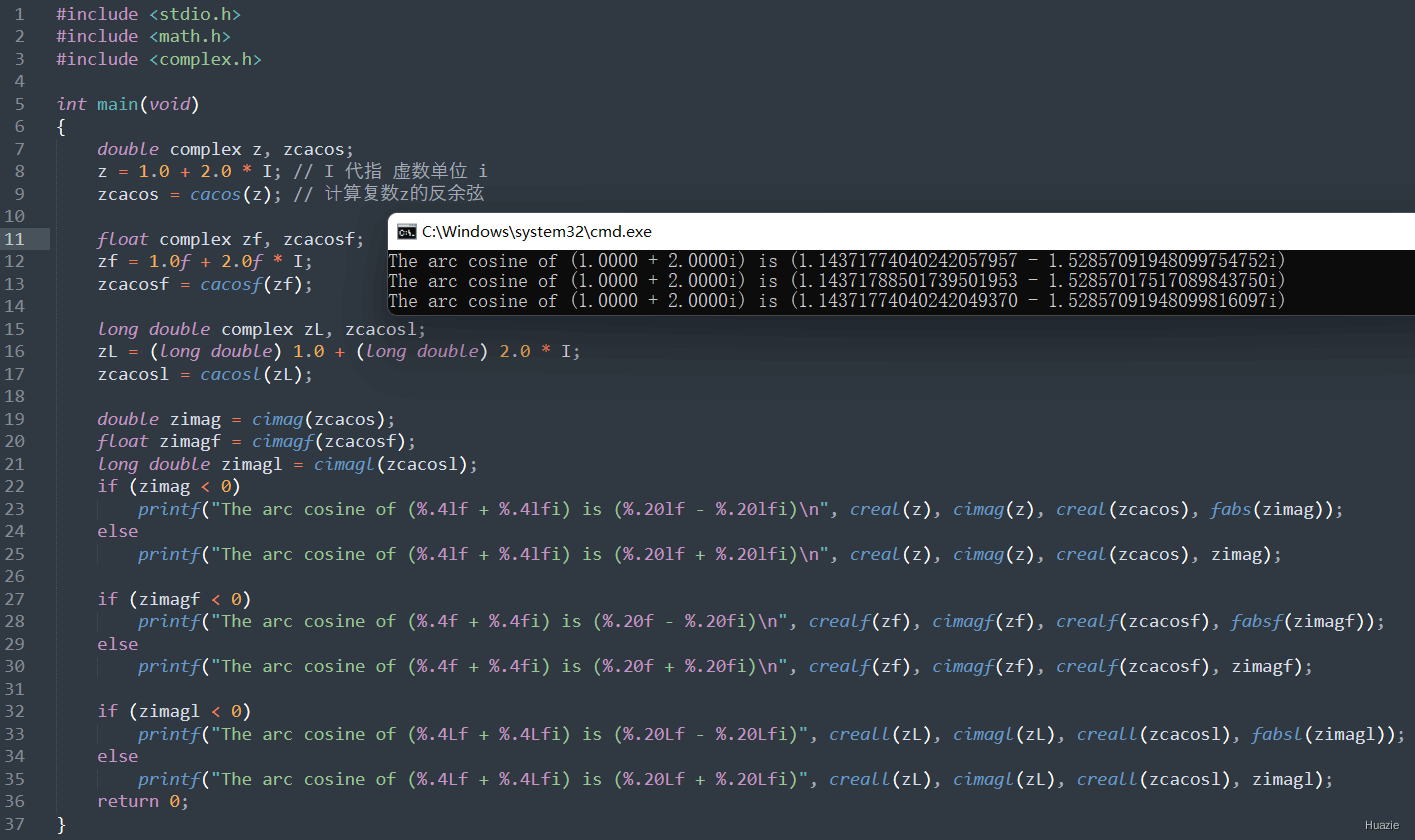
6. cacosh,cacoshf,cacoshl
6.1 函数说明
| 函数声明 | 函数功能 |
|---|---|
double complex cacosh (double complex z); |
计算复数z的反双曲余弦(double complex) |
float complex cacoshf (float complex z); |
计算复数z的反双曲余弦(float complex) |
long double complex cacoshl (long double complex z); |
计算复数z的反双曲余弦(long double complex) |
反双曲余弦函数,表示为双曲余弦函数的反函数,其定义为:对于任意实数x(x≥1),存在一个唯一的实数y,使得cosh(y) = x。此时,y就被称为x的反双曲余弦值。
6.2 演示示例
1 |
|
6.3 运行结果
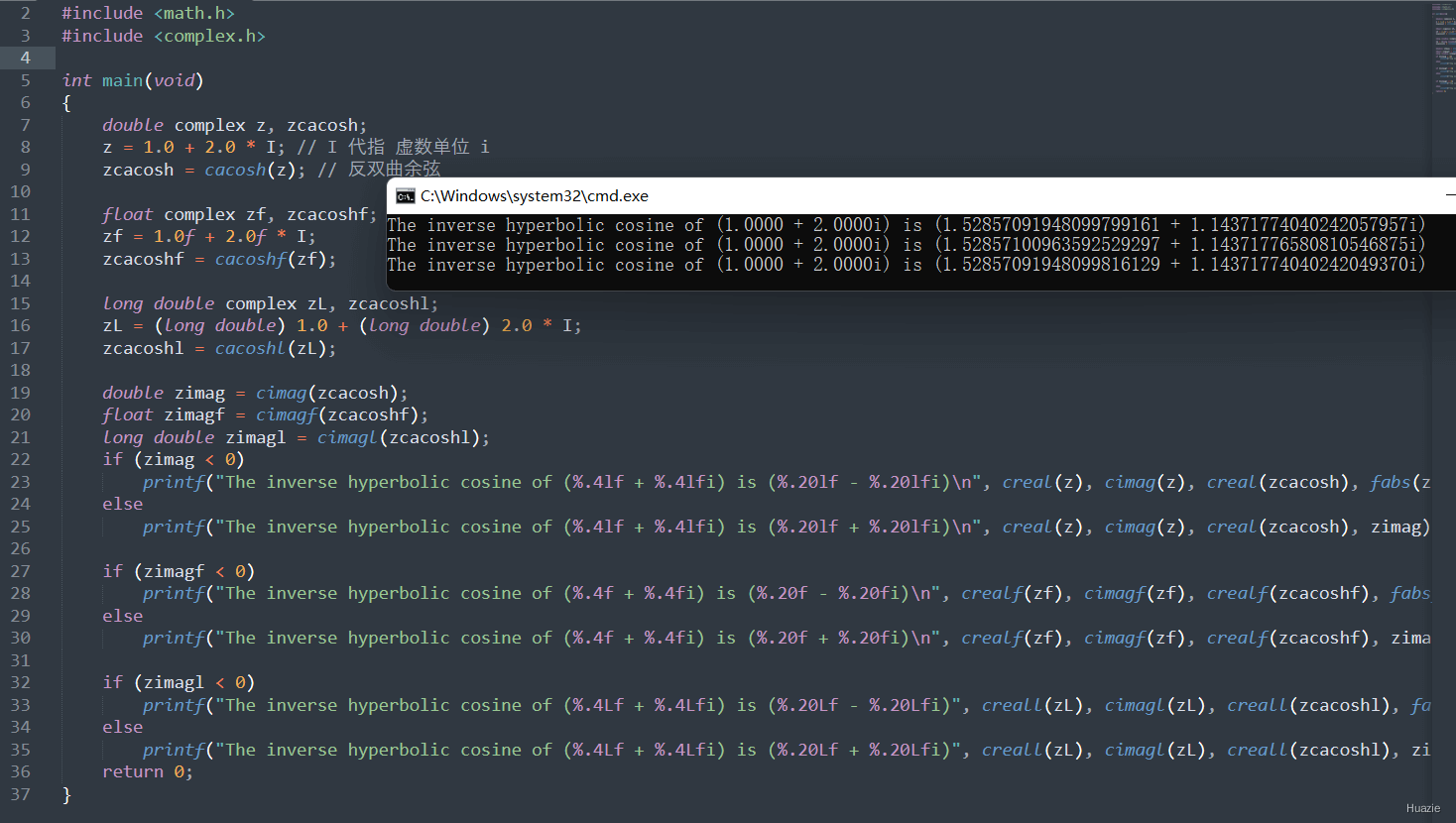
7. casin,casinf,casinl
7.1 函数说明
| 函数声明 | 函数功能 |
|---|---|
double complex casin (double complex z); |
计算复数z的反正弦(double complex) |
float complex casinf (float complex z); |
计算复数z的反正弦(float complex) |
long double complex casinl (long double complex z); |
计算复数z的反正弦(long double complex) |
反正弦函数是正弦函数的反函数。也就是说,如果sinθ=x,且x在[-1,1]的范围内,那么θ就是x的反正弦值。
7.2 演示示例
1 |
|
7.3 运行结果
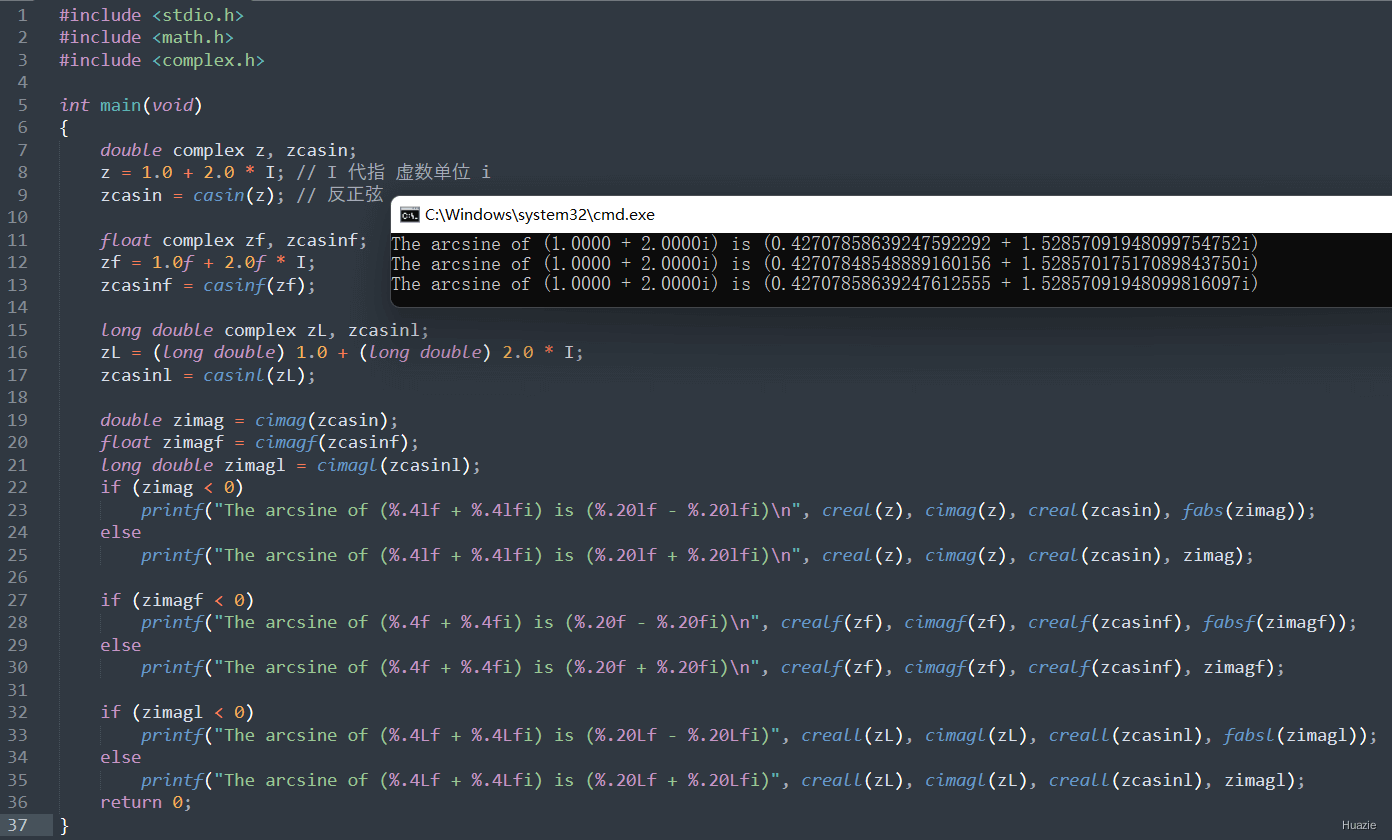
8. casinh,casinhf,casinhl
8.1 函数说明
| 函数声明 | 函数功能 |
|---|---|
double complex casinh (double complex z); |
计算复数z的反双曲正弦(double complex) |
float complex casinhf (float complex z); |
计算复数z的反双曲正弦(float complex) |
long double complex casinhl (long double complex z); |
计算复数z的反双曲正弦(long double complex) |
反双曲正弦函数是双曲正弦函数的反函数。
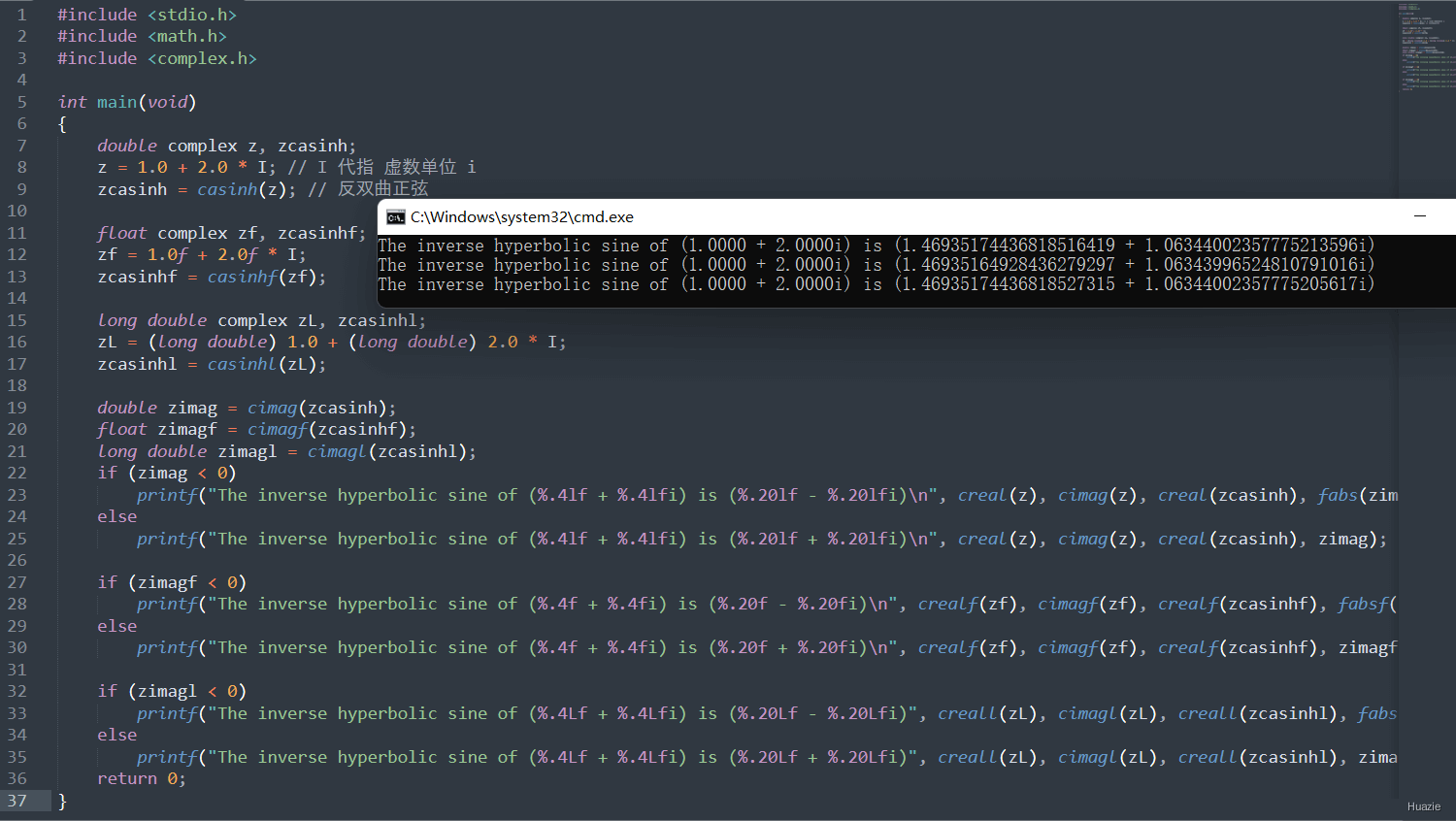
8.2 演示示例
1 |
|
8.3 运行结果
9. catan,catanf,catanl
9.1 函数说明
| 函数声明 | 函数功能 |
|---|---|
double complex catan (double complex z); |
计算复数z的反正切(double complex) |
float complex catanf (float complex z); |
计算复数z的反正切(float complex) |
long double complex catanl (long double complex z); |
计算复数z的反正切(long double complex) |
反正切函数是正切函数的反函数。如果给定一个正切值x,反正切函数会返回对应的角度值θ,该角度值θ满足tan(θ)=x,并且θ在(-π/2, π/2)范围内。
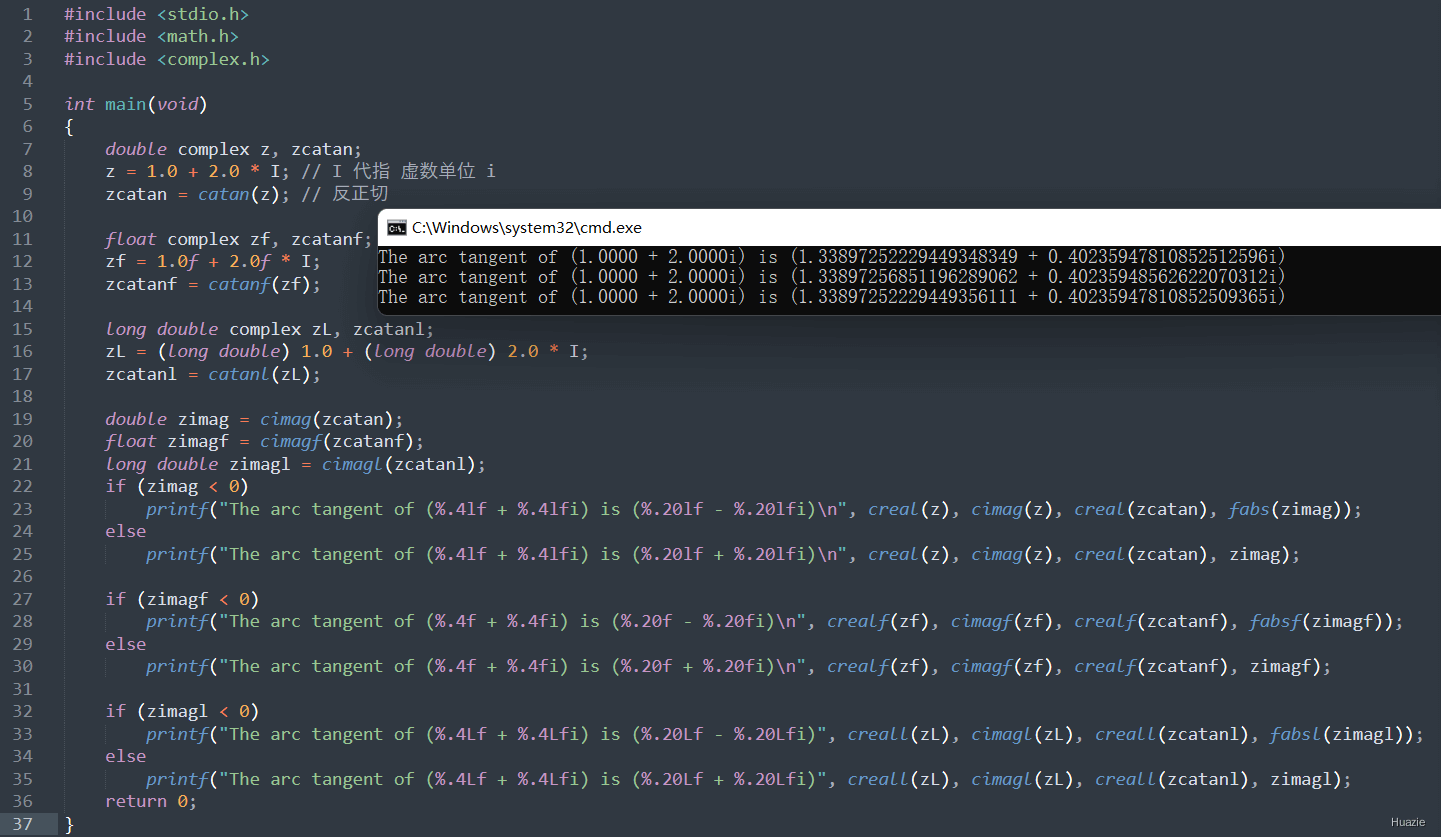
9.2 演示示例
1 |
|
9.3 运行结果
10. catanh,catanhf,catanhl
10.1 函数说明
| 函数声明 | 函数功能 |
|---|---|
double complex catanh (double complex z); |
计算复数z的反双曲正切(double complex) |
float complex catanhf (float complex z); |
计算复数z的反双曲正切(float complex) |
long double complex catanhl (long double complex z); |
计算复数z的反双曲正切(long double complex) |
反双曲正切函数是双曲正切函数的反函数。
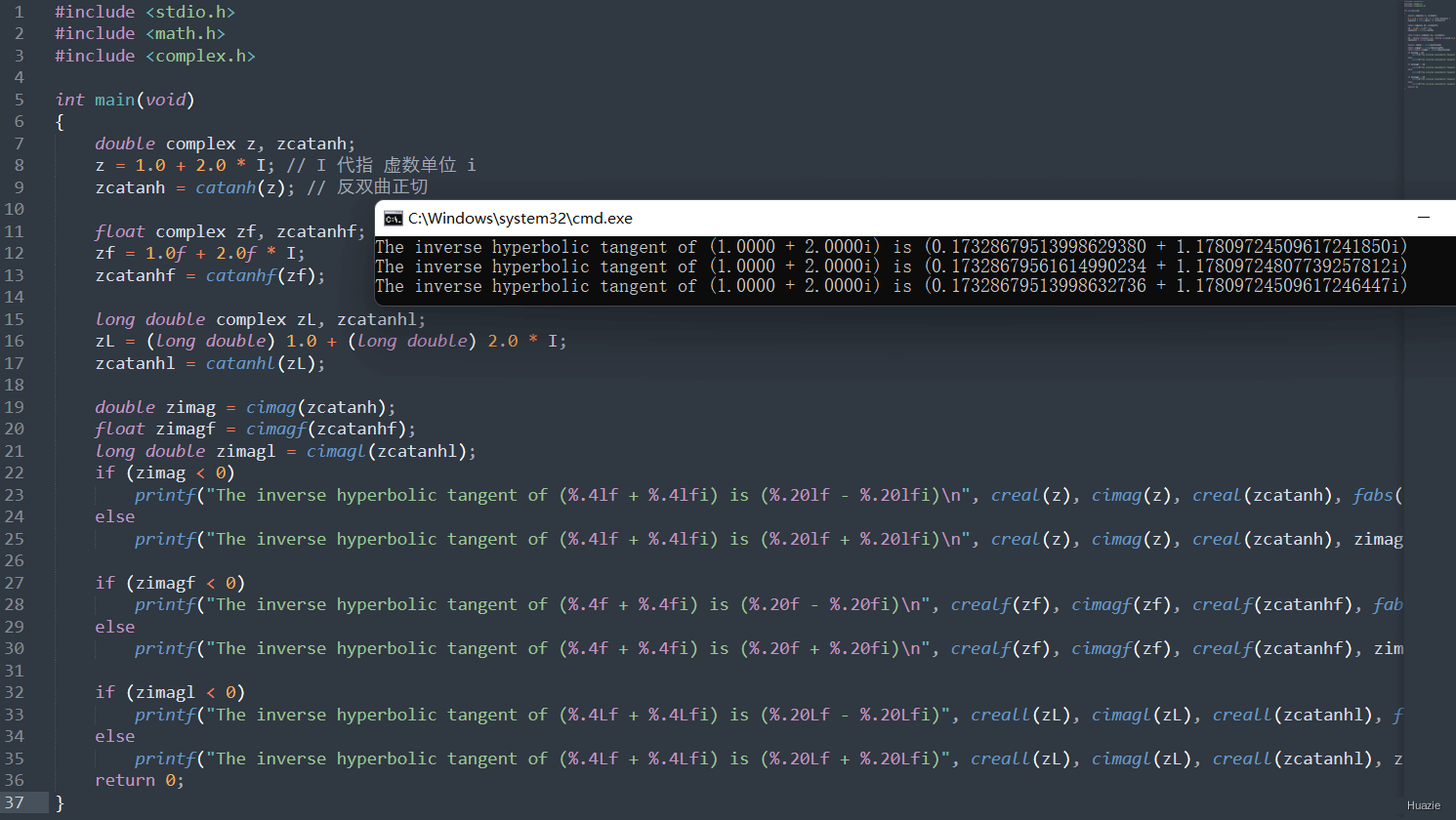
10.2 演示示例
1 |
|
10.3 运行结果
11. ccos,ccosf,ccosl
11.1 函数说明
| 函数声明 | 函数功能 |
|---|---|
double complex ccos (double complex z); |
计算复数z的余弦(double complex) |
float complex ccosf (float complex z); |
计算复数z的余弦(float complex) |
long double complex ccosl (long double complex z); |
计算复数z的余弦(long double complex) |
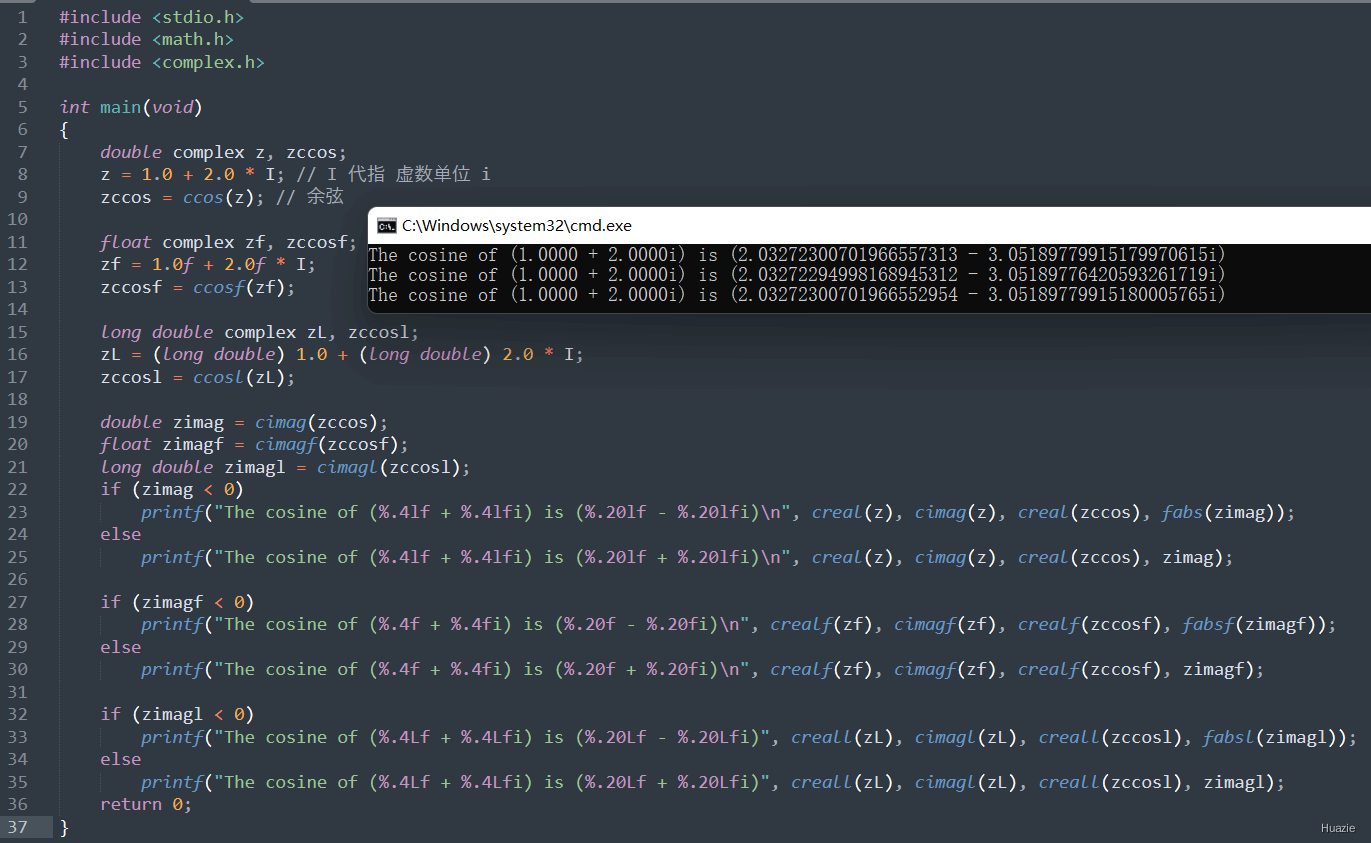
11.2 演示示例
1 |
|
11.3 运行结果
12. ccosh,ccoshf,ccoshl
12.1 函数说明
| 函数声明 | 函数功能 |
|---|---|
double complex ccosh (double complex z); |
计算复数z的双曲余弦(double complex) |
float complex ccoshf (float complex z); |
计算复数z的双曲余弦(float complex) |
long double complex ccoshl (long double complex z); |
计算复数z的双曲余弦(long double complex) |
12.2 演示示例
1 |
|
12.3 运行结果
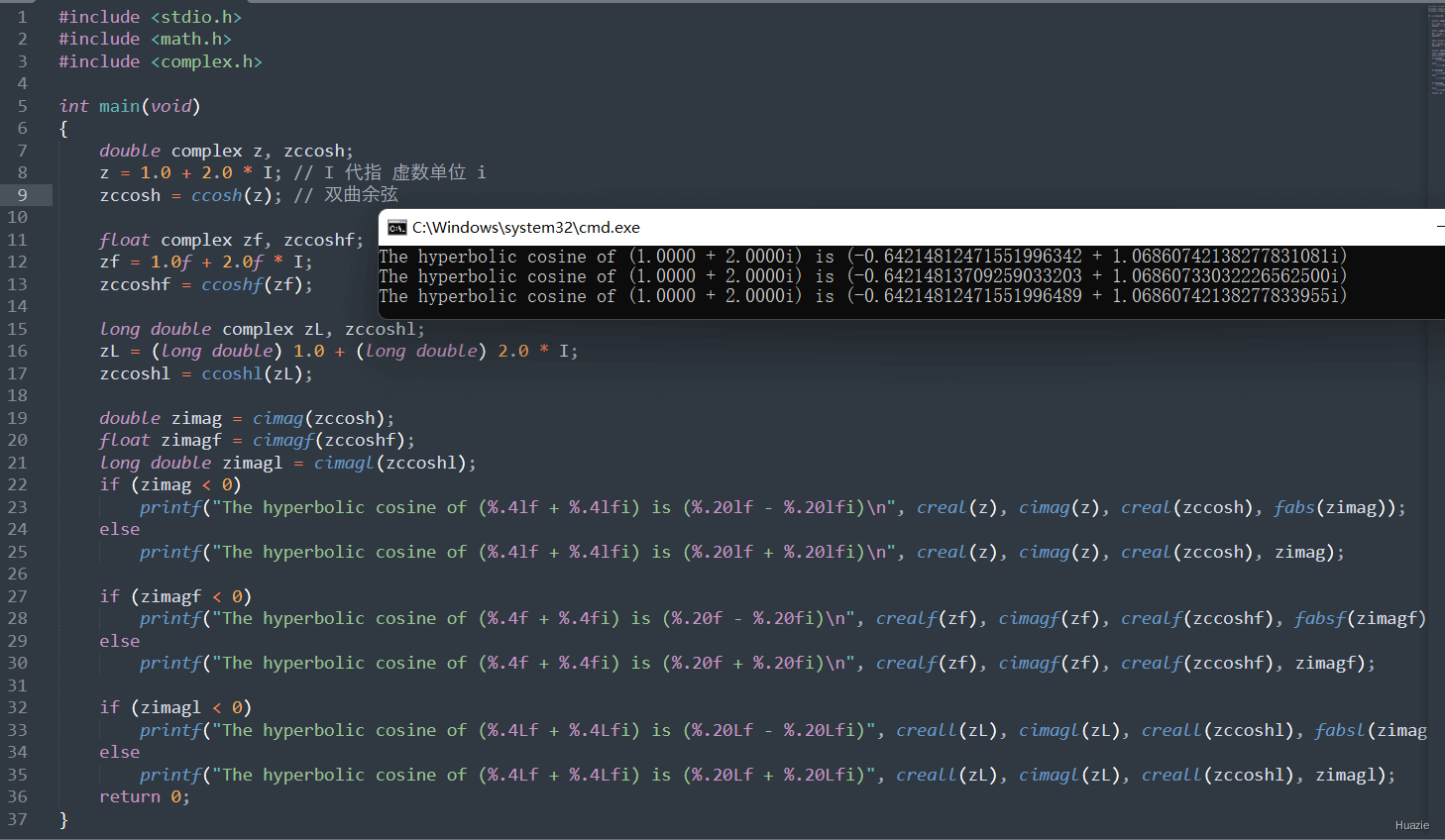
13. csin,csinf,csinl
13.1 函数说明
| 函数声明 | 函数功能 |
|---|---|
double complex csin (double complex z); |
计算复数z的正弦(double complex) |
float complex csinf (float complex z); |
计算复数z的正弦(float complex) |
long double complex csinl (long double complex z); |
计算复数z的正弦(long double complex) |
13.2 演示示例
1 |
|
13.3 运行结果
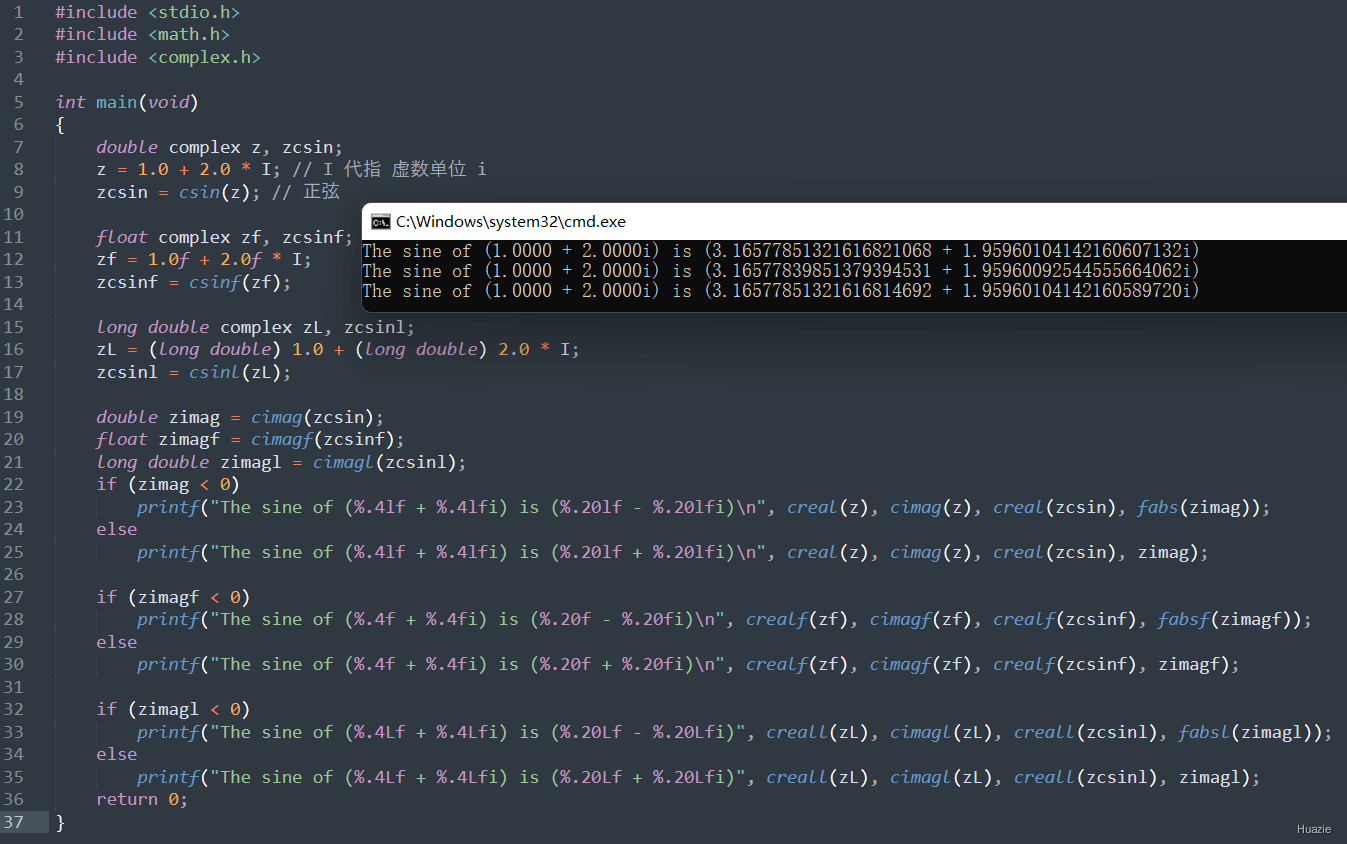
14. csinh,csinhf,csinhl
14.1 函数说明
| 函数声明 | 函数功能 |
|---|---|
double complex csinh (double complex z); |
计算复数z的双曲正弦(double complex) |
float complex csinhf (float complex z); |
计算复数z的双曲正弦(float complex) |
long double complex csinhl (long double complex z); |
计算复数z的双曲正弦(long double complex) |
14.2 演示示例
1 |
|
14.3 运行结果
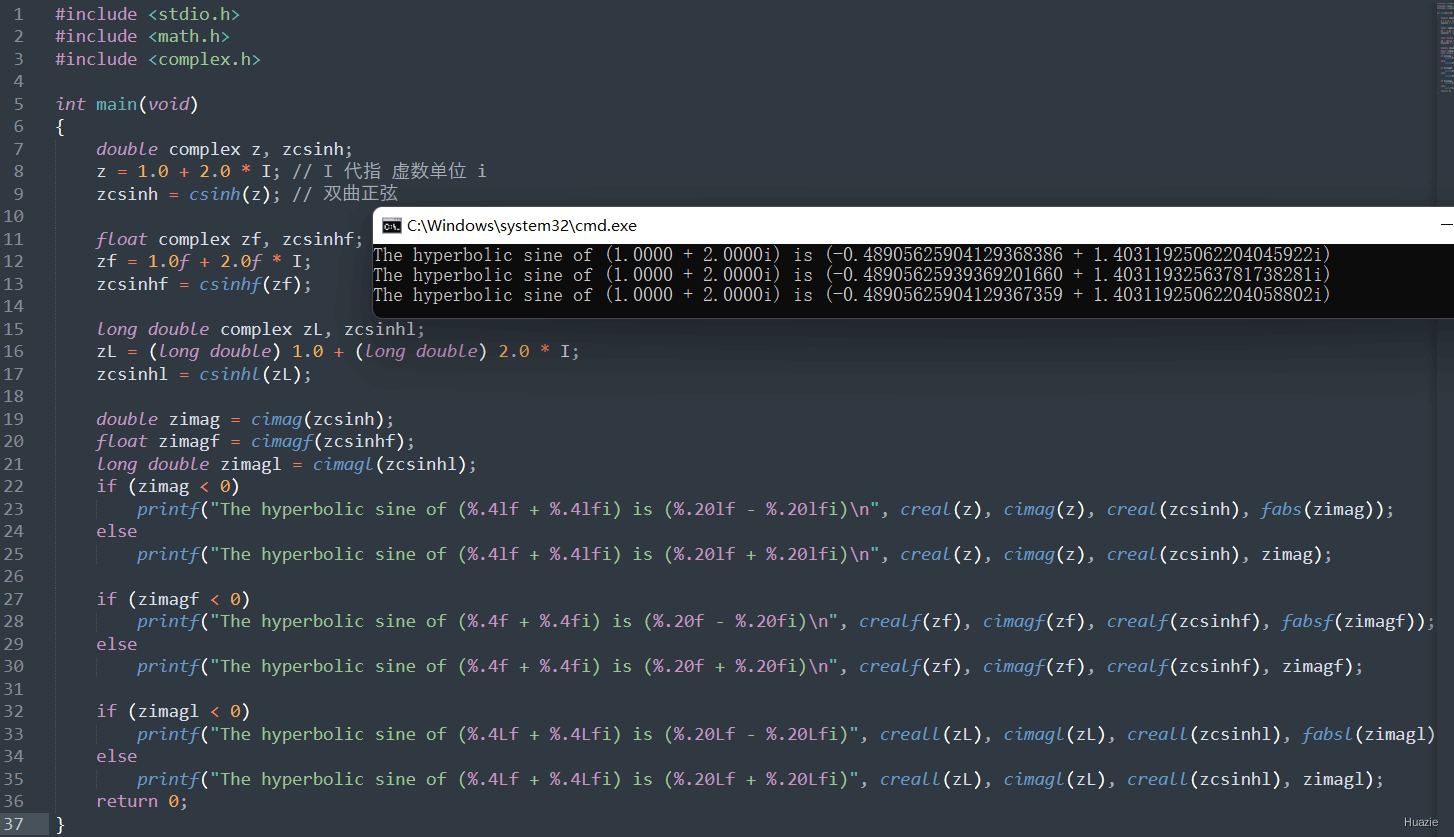
15. ctan,ctanf,ctanl
15.1 函数说明
| 函数声明 | 函数功能 |
|---|---|
double complex ctan (double complex z); |
计算复数z的正切(double complex) |
float complex ctanf (float complex z); |
计算复数z的正切(float complex) |
long double complex ctanl (long double complex z); |
计算复数z的正切(long double complex) |
15.2 演示示例
1 |
|
15.3 运行结果
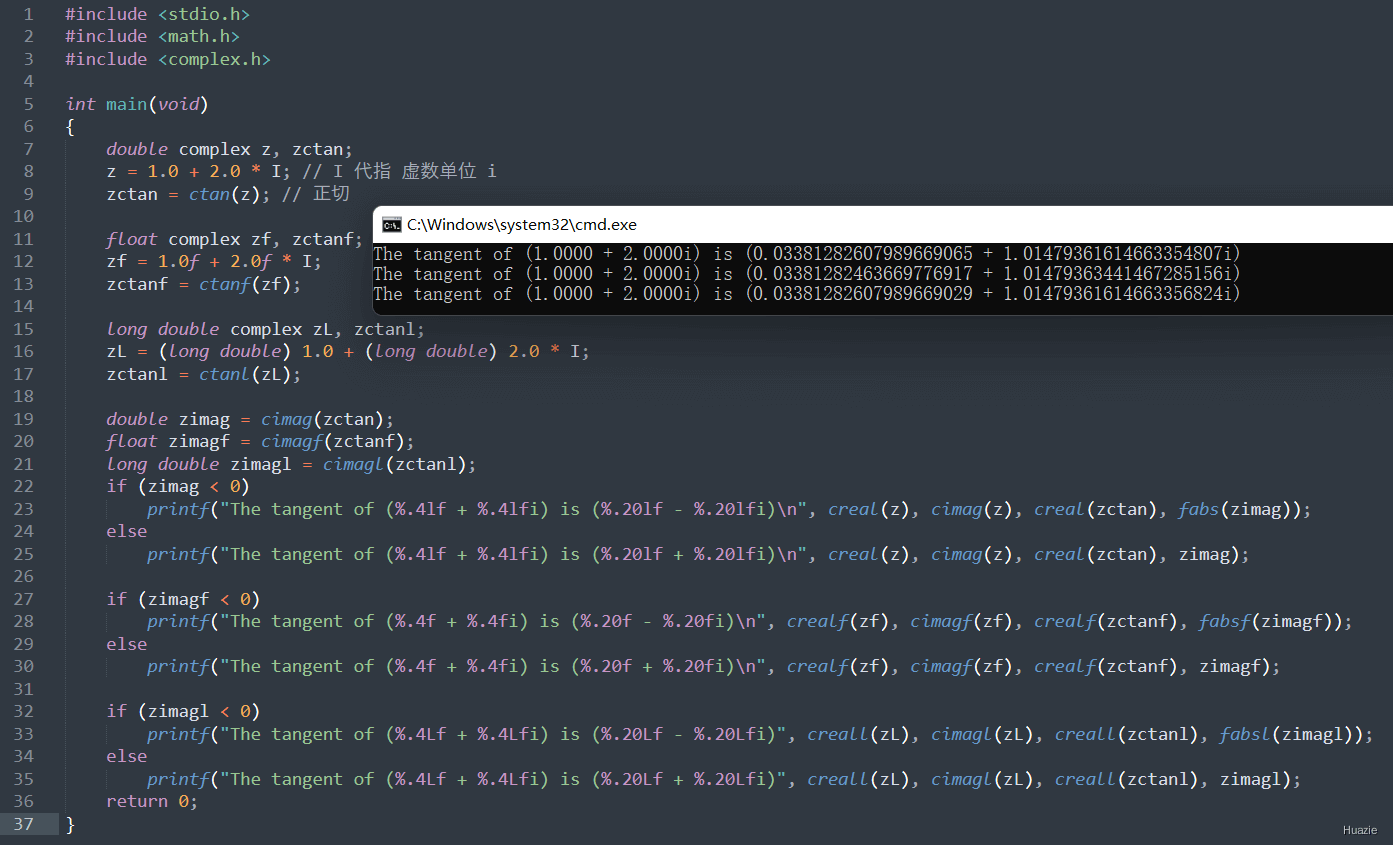
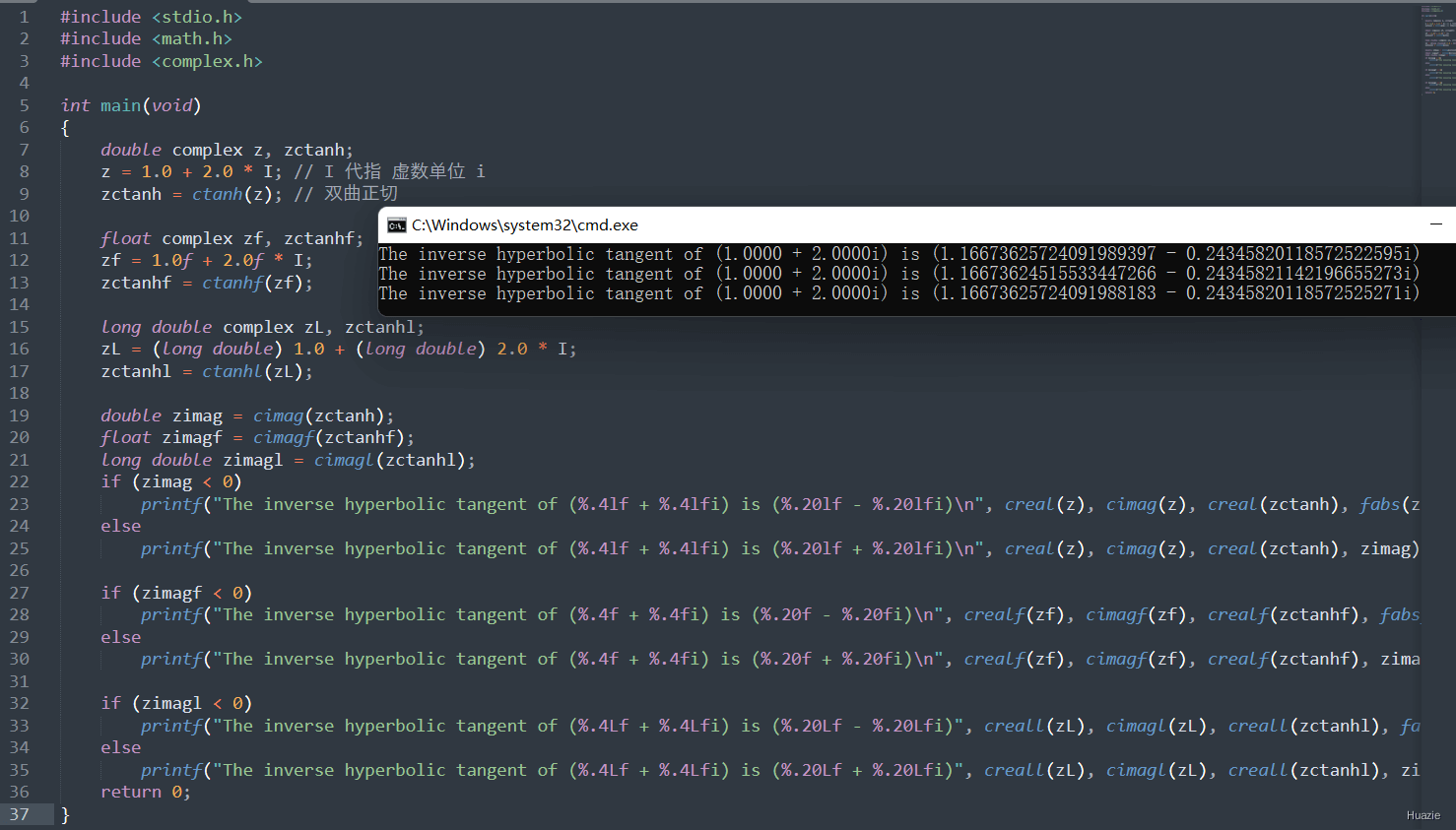
16. ctanh,ctanhf,ctanhl
16.1 函数说明
| 函数声明 | 函数功能 |
|---|---|
double complex ctanh (double complex z); |
计算复数z的双曲正切(double complex) |
float complex ctanhf (float complex z); |
计算复数z的双曲正切(float complex) |
long double complex ctanhl (long double complex z); |
计算复数z的双曲正切(long double complex) |
16.2 演示示例
1 |
|
16.3 运行结果
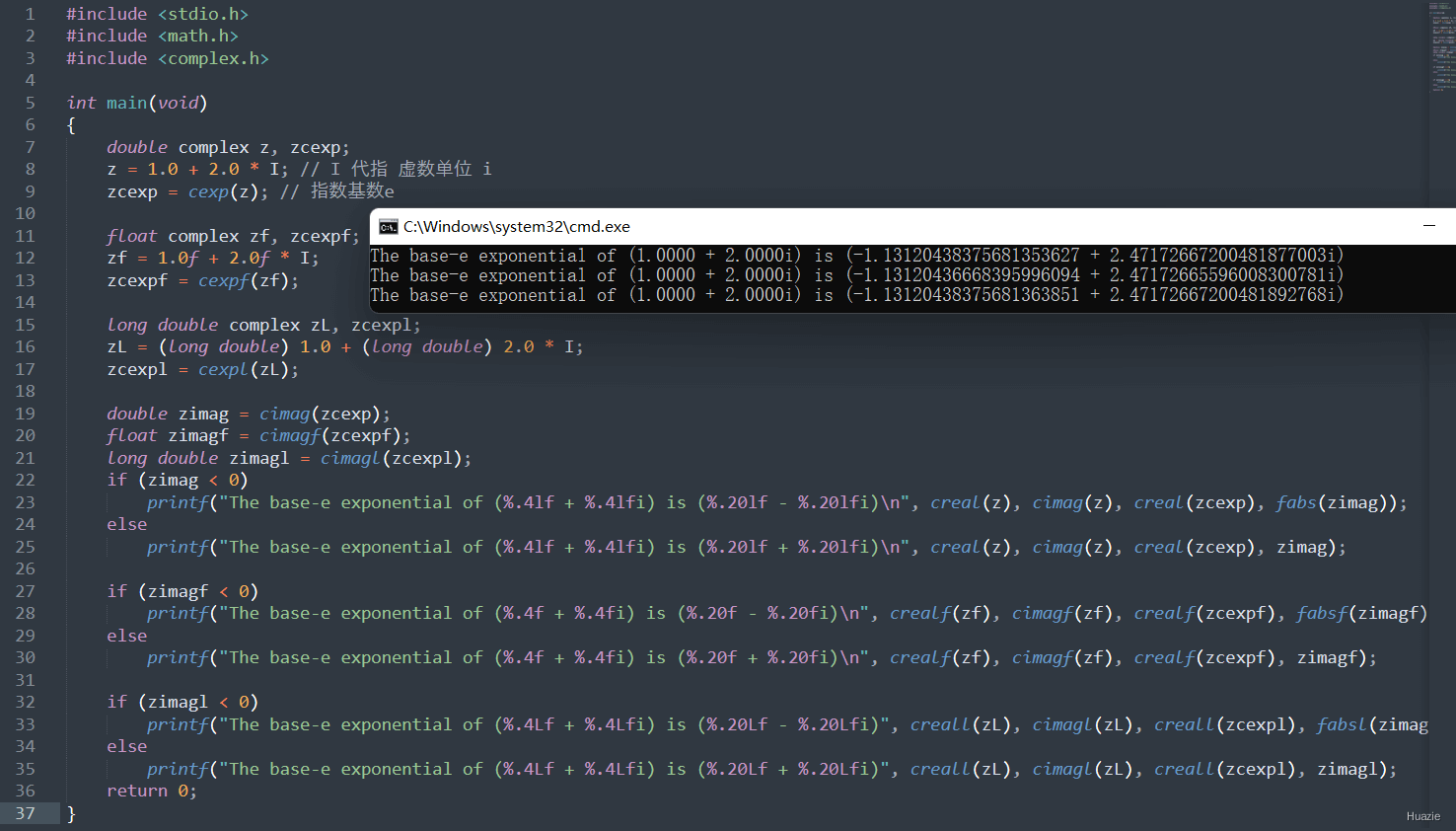
17. cexp,cexpf,cexpl
17.1 函数说明
| 函数声明 | 函数功能 |
|---|---|
double complex cexp (double complex z); |
计算复数z的指数基数e(double complex) |
float complex cexpf (float complex z); |
计算复数z的指数基数e(float complex) |
long double complex cexpl (long double complex z); |
计算复数z的指数基数e(long double complex) |
17.2 演示示例
1 |
|
17.3 运行结果
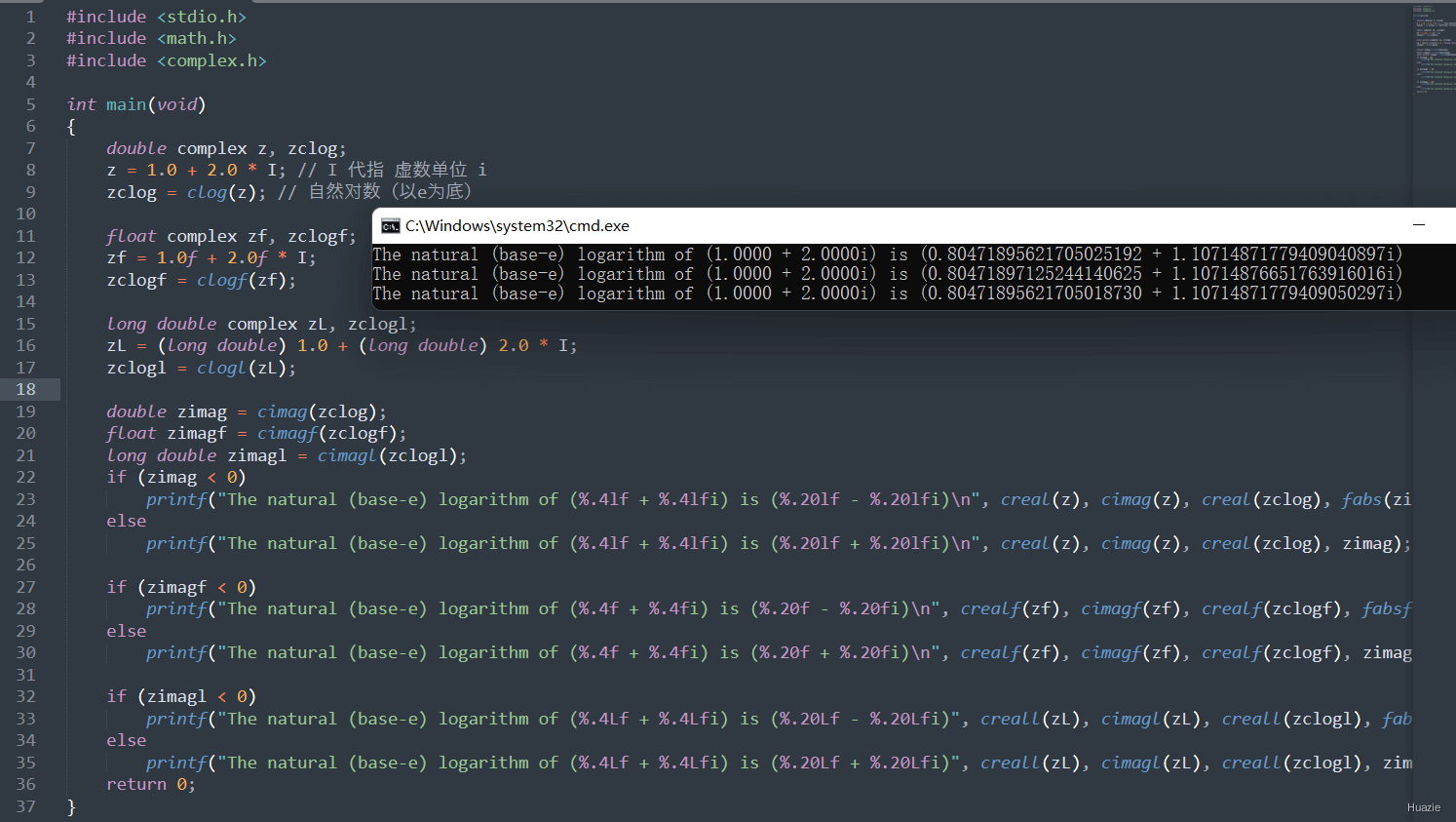
18. clog,clogf,clogl
18.1 函数说明
| 函数声明 | 函数功能 |
|---|---|
double complex clog (double complex z); |
计算复数z的自然对数(以e为底)(double complex) |
float complex clogf (float complex z); |
计算复数z的自然对数(以e为底)(float complex) |
long double complex clogl (long double complex z); |
计算复数z的自然对数(以e为底)(long double complex) |
18.2 演示示例
1 |
|
18.3 运行结果
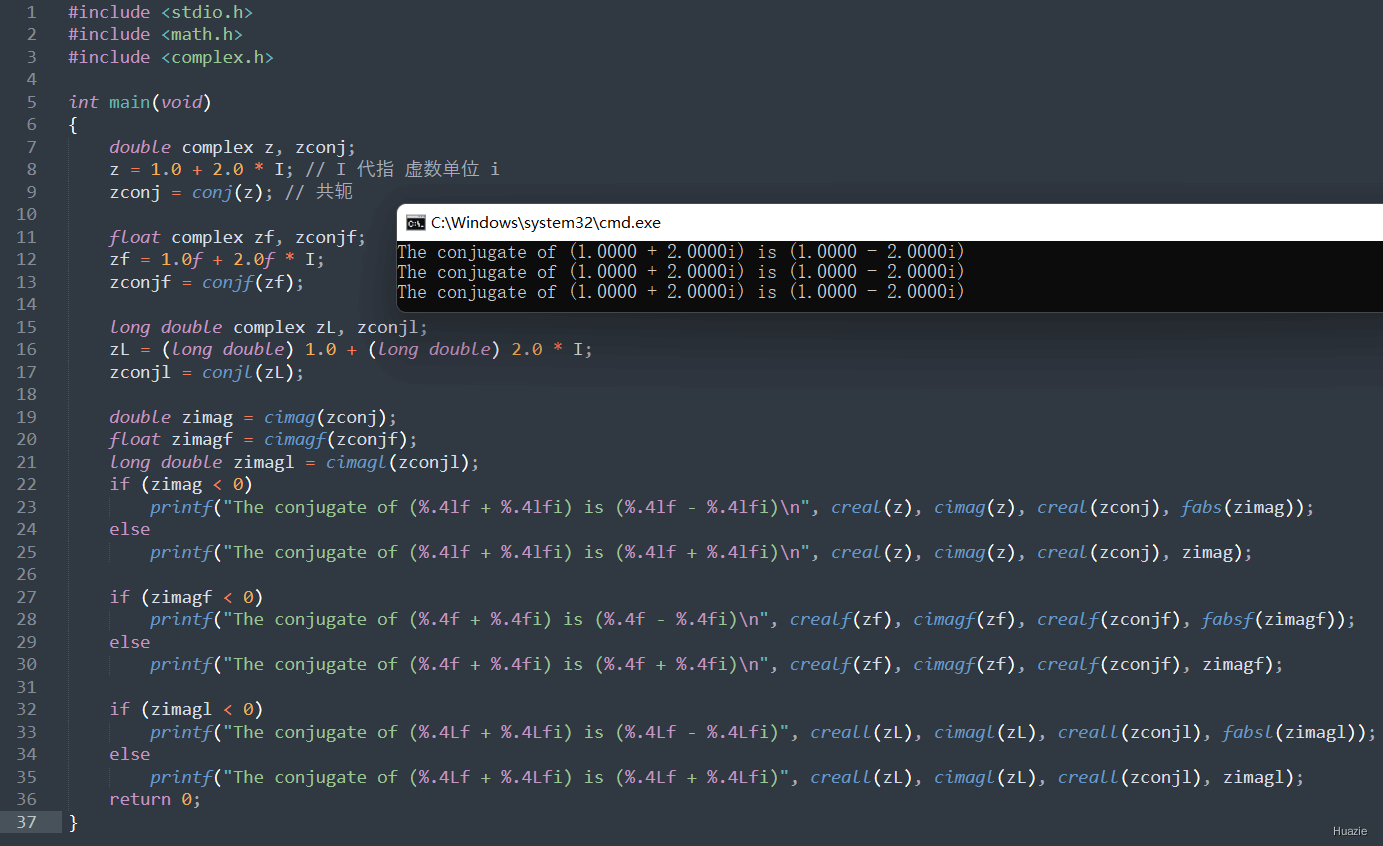
19. conj,conjf,conjl
19.1 函数说明
| 函数声明 | 函数功能 |
|---|---|
double complex conj (double complex z); |
计算复数z的共轭(double complex) |
float complex conjf (float complex z); |
计算复数z的共轭(float complex) |
long double complex conjl (long double complex z); |
计算复数z的共轭(long double complex) |
19.2 演示示例
1 |
|
19.3 运行结果
20. cpow,cpowf,cpowl
20.1 函数说明
| 函数声明 | 函数功能 |
|---|---|
double complex cpow (double complex x, double complex y); |
计算x的y次方值 (double complex) |
float complex cpowf (float complex x, float complex y); |
计算x的y次方值 (float complex) |
long double complex cpowl (long double complex x, long double complex y); |
计算x的y次方值 (double complex) |
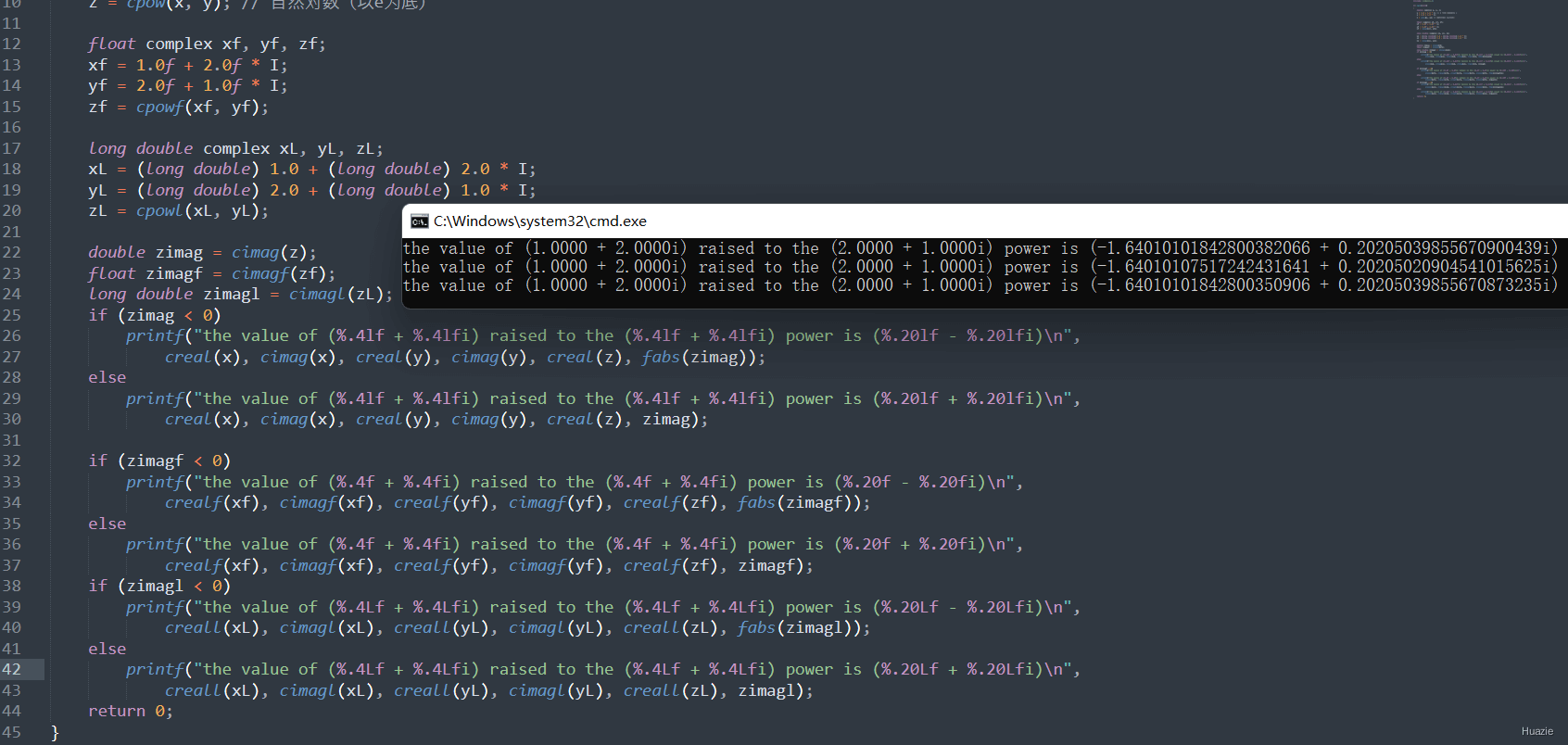
20.2 演示示例
1 |
|
20.3 运行结果
21. cproj,cprojf,cprojl
21.1 函数说明
| 函数声明 | 函数功能 |
|---|---|
double complex cproj (double complex z); |
计算复数z在黎曼球面上的投影(double complex) |
float complex cprojf (float complex z); |
计算复数z在黎曼球面上的投影(float complex) |
long double complex cprojl (long double complex z); |
计算复数z在黎曼球面上的投影(long double complex) |
黎曼球面上的投影是一种将三维空间中的黎曼球面与二维复平面通过立体投影方式建立一一对应关系的映射。
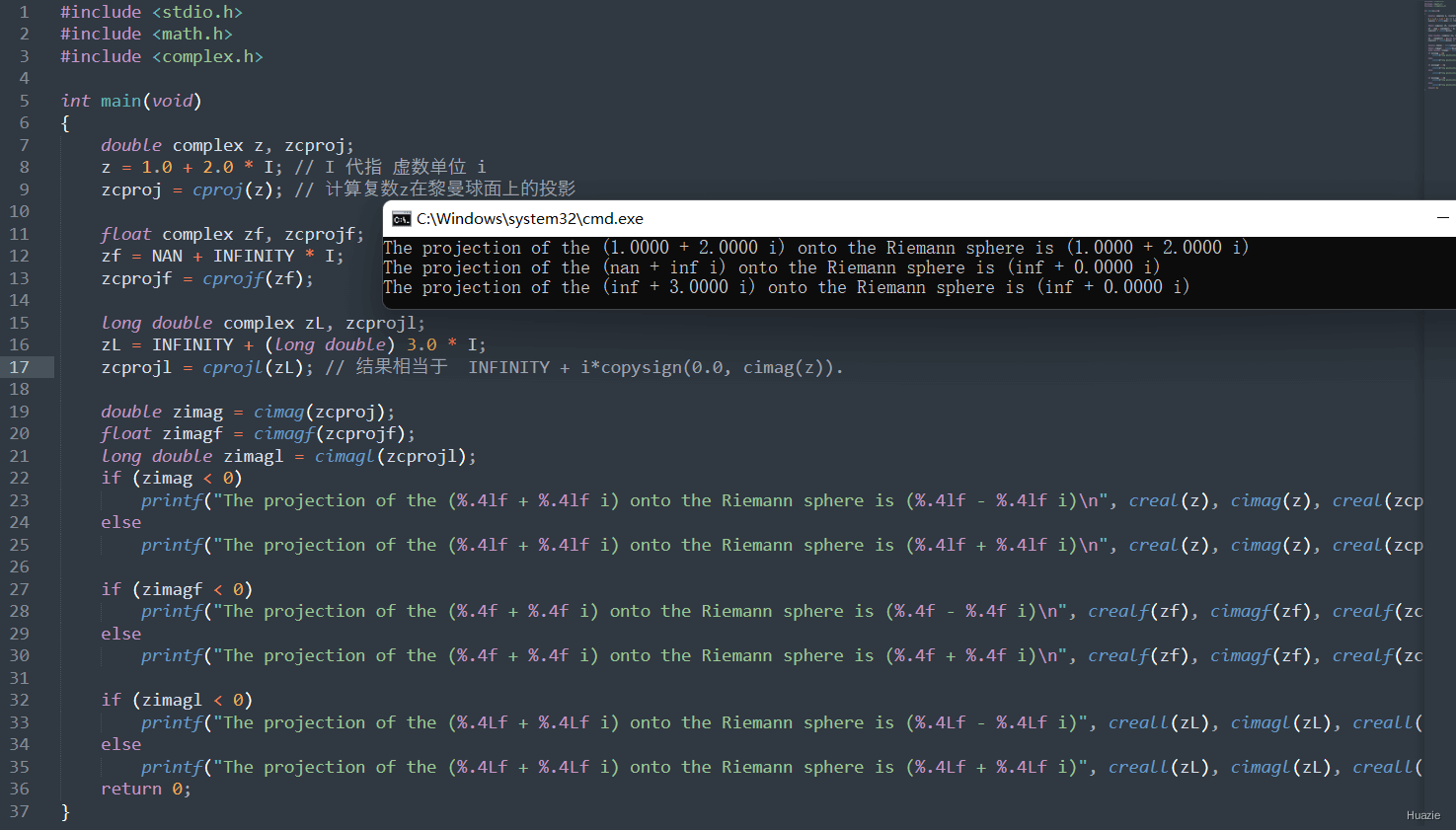
21.2 演示示例
1 |
|
21.3 运行结果
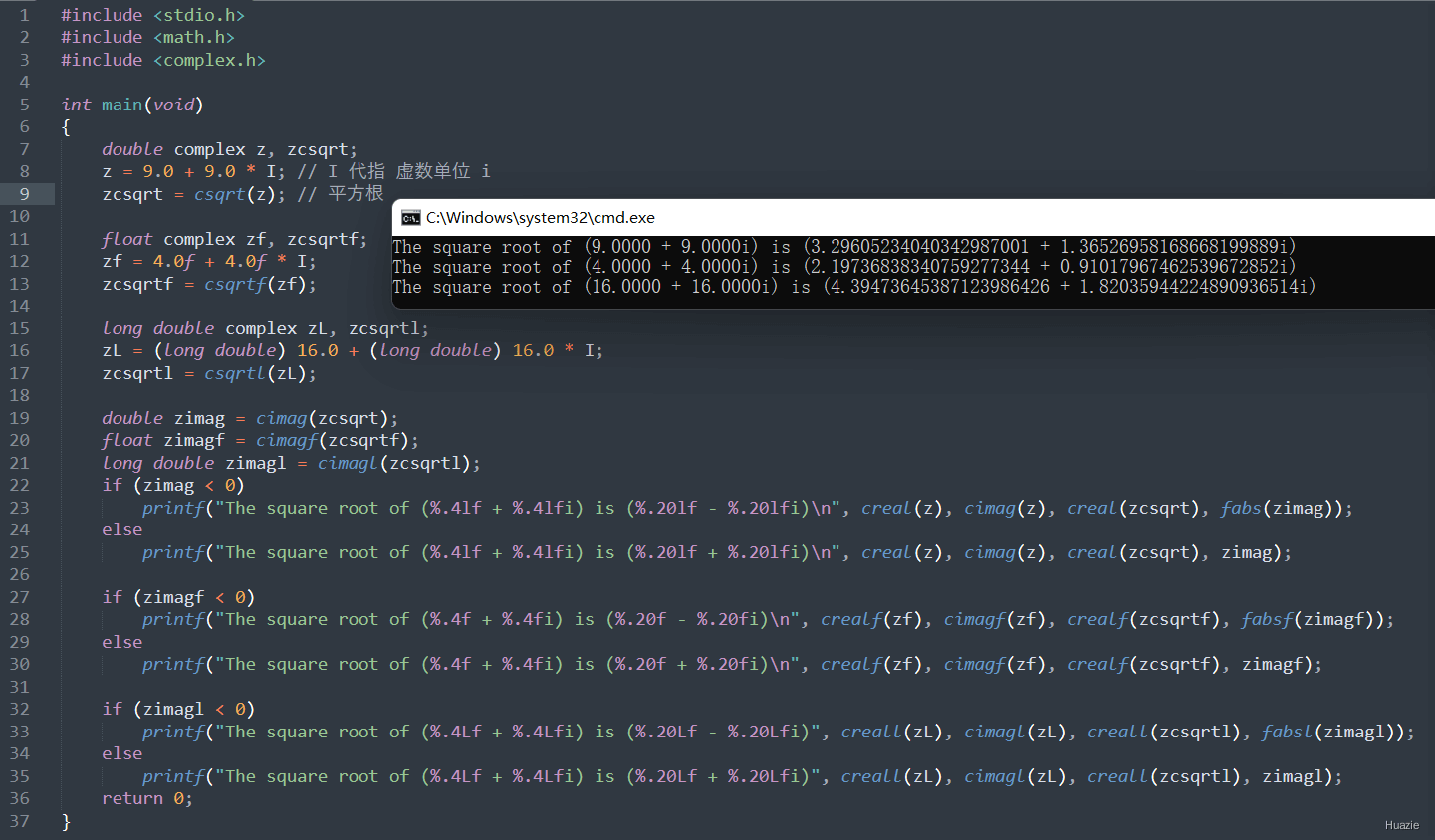
22. csqrt,csqrtf,csqrtl
22.1 函数说明
| 函数声明 | 函数功能 |
|---|---|
double complex csqrt (double complex z); |
计算复数z的平方根(double complex) |
float complex csqrtf (float complex z); |
计算复数z的平方根(float complex) |
long double complex csqrtl (long double complex z); |
计算复数z的平方根(long double complex) |
22.2 演示示例
1 |
|
22.3 运行结果